LA MEDIA ARITMÉTICA
En matemáticas y estadística, la media aritmética, también llamada promedio o media, de un conjunto finito de números es el valor característico de una serie de datos cuantitativos, objeto de estudio que parte del principio de la esperanza matemática o valor esperado, se obtiene a partir de la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadisticos muestrales
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos
Ejemplo 1:
Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.
Ejemplo 2:
La edad de 8 amigos son: 33; 27; 29; 27; 30; 33; 36 y 20 años. Hallar la edad promedia.
LA MEDIA PONDERADA
La media ponderada (MP) es una medida de centralizazcion. Consiste en otorgar a cada observación del conjunto de datos (X1,X2,…,XN) unos pesos (p1,p2,…,pN) según la importancia de cada elemento.
Cuanto más grande sea el peso de un elemento, más importante se considera que es éste.
La media ponderada tiene numerosas aplicaciones, por ejemplo, la nota de una asignatura donde el examen final tiene un peso mayor al de un trabajo. O en el cálculo del IPC (Índice de Precios de Consumo). El IPC es un indicador de los precios de los bienes y servicios básicos que consume la población. Para calcularlo, se otorga pesos a los diferentes bienes (pan, fruta, vivienda,…) y se calcula la media ponderada.
La media aritmética es un caso particular de media ponderada, en la que todos los pesos son uno, ya que a todos los elementos se les otorga la misma importancia.
Ejemplo 1:
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media y la media ponderada
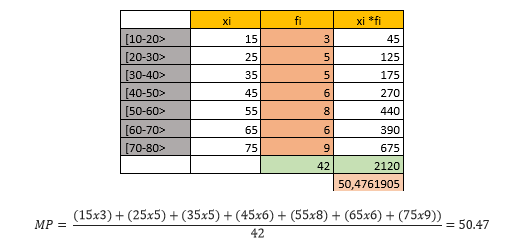
Ejemplo 2:
Tomamos cuatro elementos evaluables y calculamos la nota final de una asignatura usando la media ponderada de las notas que han obtenido el alumno. Damos diferentes pesos según la importancia de la siguiente forma: un peso de 3 al examen inicial, de 1 al trabajo entregable, 2 al trabajo final y 4 al examen final. En la tabla siguiente se muestra las notas de un alumno y sus pesos:
LA MEDIA GEOMÉTRICA
La media geométrica (MG) de un conjunto de números estrictamente positivos (X1, X2,…,XN) es la raíz N-ésima del producto de los N elementos.
Todos los elementos del conjunto tienen que ser mayores que cero. Si algún elemento fuese cero (Xi=0), entonces la MG sería 0 aunque todos los demás valores estuviesen alejados del cero.
La media geométrica es útil para calcular medias de porcentajes, tantos por uno, puntuaciones o índices. Tiene la ventaja de que no es tan sensible como la media a los valores extremos.
Ejemplo 1:
Calcular la media geométrica del número de hermanos que tienen Berta, Borja y Diana si tienen 15; 17 y 10 respectivamente.
Aplicamos la fórmula:
Ejemplo 2:
En una empresa quieren saber la proporción media de mujeres en los diferentes departamentos. Para ello, se recoge el porcentaje de mujeres en los cinco principales departamentos.
LA MEDIA ARMÓNICA
La media armónica se define como el recíproco de la media aritmética de los recíprocos:
Esta medida se emplea para promediar variaciones con respecto al tiempo tales como productividades, tiempos, rendimientos, cambios, etc.,
Ejemplo 1:
Hallar la media armónica de los números 4, 5, 7 y 8.
Ejemplo 2:
Un obrero puede pintar una casa en 6 días y otro puede pintarla en 8 días. Hallar el rendimiento promedio que se tendría que tardar en pintar la misma casa cualquier obrero, tomando como base el desempeño de estos dos.
Comments