SEMANA 09:
REGRESIÓN LINEAL MÚLTIPLE
La regresión lineal es una técnica estadística destinada a analizar las causas de por qué pasan las cosas. A partir de los análisis de regresión lineal múltiple podemos:
-
identificar que variables independientes (causas) explican una variable dependiente (resultado)
-
comparar y comprobar modelos causales
-
predecir valores de una variable, es decir, a partir de unas características predecir de forma aproximada un comportamiento o estado

ejercicios

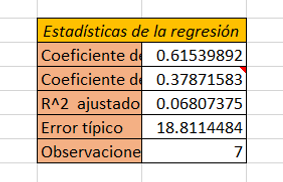
Ahora hallaremos el analisis estadístico, tomando solo las dos primeras variables para hallar el indice de correlación de la regresion
ejemplo 02:
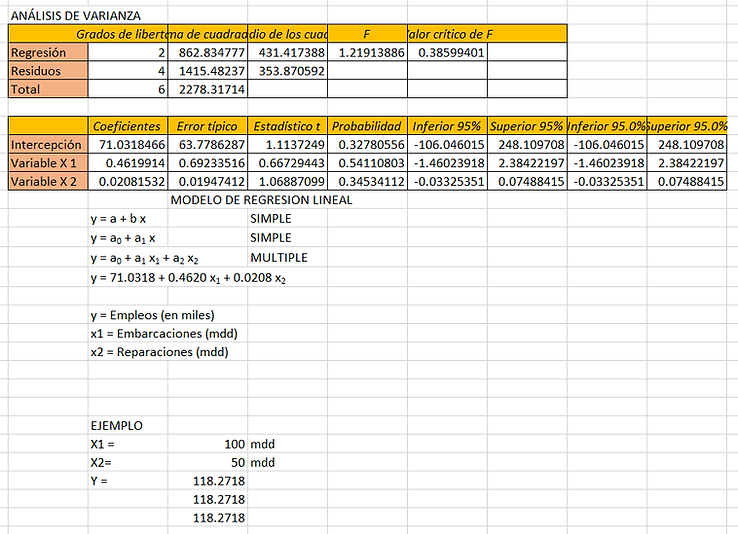
interpretación de los resultados de una regresión lineal múltiple
El primer cuadro de resultados proporciona los coeficientes de ajuste del modelo. El R’² (coeficiente de determinación) proporciona una idea del % de variabilidad de la variable a modelizar, explicado por las variables explicativas. Mientras más cerca está de 1 este coeficiente, mejor es el modelo.

En nuestro caso, 63% de la variabilidad es explicada por la estatura y la edad. El resto de la variabilidad es debido a efectos (variables explicativas) que no son tenidos en cuenta en este ejemplo. En el tutorial sobre la regresión simple, hemos visto que el uso de la estatura en el modelo ya explicaba 60%. La contribución de la variable edad es entonces escasa.
El cuadro de análisis de la varianza es un resultado que debe ser atentamente analizado (ver a continuación). Es en este nivel que comprobamos si podemos considerar que las variables explicativas seleccionadas (la estatura y la edad) originan una cantidad de información significativa al modelo (hipótesis nula H0) o no. En otros términos, es una manera de comprobar si la media de la variable a modelizar (el peso) bastaràa con describir los resultados obtenidos o no.

La prueba del F de Fisher es utilizada. Dado que la probabilidad asociada al F, en este caso, es inferior de 0.0001, significa que nos arriesgamos de menos del 0.01% concluyendo que las variables explicativas originan una cantidad de información significativa al modelo.
La tabla siguiente exhibe los resultados "Type III SS". Estos resultados indican si una variable trae información significativa o no, una vez que todas las otras variables estan incluidas en el modelo.

El siguiente cuadro proporciona los detalles sobre el modelo y es esencial en cuanto el modelo debe ser utilizado para realizar previsiones, simulaciones o si debe ser comparado a otros resultados, por ejemplo los coeficientes que obtendràamos para los varones. Vemos que el p-value asociado a la prueba de Student para la edad es aproximadamente de 0.01, y que el intervalo de confianza de 95% asociado roza el valor 0. Eso corrobora el escaso impacto de la edad sobre el modelo. La ecuación del modelo es proporcionada abajo del cuadro. El modelo enseña que en los làmites proporcionadas por las observaciones del intervalo de la variable estatura y de la variable edad, cada vez que la estatura aumenta de un inch, el peso aumenta de 3.1 libras, y cada vez que la edad aumenta de un mes, el peso aumenta de 0.23 libras.

La tabla y el gráfico abajo corresponden a los coeficientes de regresión estandarizados (designados a veces coeficientes beta). Permiten comparar directamente la influencia relativa de las variables explicativas sobre la variable dependiente, y ellas significatividad.

el cuadro siguiente expone el análisis de los residuos. Los residuos centrados reducidos deben tener una atención particular, dado que las hipótesis vinculadas a la regresión lineal, deben ser distribuidos según una ley normal N(0,1). Eso significa, entre otros, que 95% de los residuos deben encontrarse en el intervalo [-1.96, 1.96]. Dado que el escaso número de datos del que disponemos aquà, cualquier valor fuera de este intervalo es revelador de un dato sospechoso. Hemos utilizado la herramienta DataFlagger de XLSTAT, con el fin de demostrar rápidamente los valores que se encuentran fuera del intervalo [-1.96, 1.96].
Podemos aquà identificar ocho observaciones dudosas sobre 237 observaciones, o sea 6.3% en vez de 5%.
El gráfico siguiente permite visualizar las predicciones y las observaciones.

El histograma de los residuos estandarizados permite señalar rápidamente y visualmente la presencia de valores fuera del intervalo [-2, 2].
