SEMANA 06:
- huamanpulloj26
- 27 abr 2019
- 5 Min. de lectura
MEDIDAS DE POSICIÓN:
Las medidas de posición relativa se llaman en general cuantiles y se pueden clasificar en tres grandes grupos: Cuartiles, quintiles, deciles, percentiles.
Las medidas de posición como los cuartiles, quintiles, deciles y percentiles dividen a una distribución ordenada en partes iguales. Para calcular las medidas de posición es necesario que los datos estén ordenados de menor a mayor.
Los Cuartiles (Qn):
son los tres valores de la variable de una distribución que la dividen en cuatro partes iguales, es decir, al 25%, 50% y 75%. Para calcular el valor de uno de los cuatro Cuartiles, se utiliza la formula:
Qk = k (n/4) En donde: Qk = Cuartil número 1, 2, 3 ó 4 n = total de datos de la distribución. Se advierte que la posición del segundo cuartil corresponde a la ubicación de la mediana, es decir que el segundo cuartil será siempre igual a la mediana. Para calcular los cuartiles (datos no agrupados) debes seguir los siguientes pasos: 1º Se ordenan los datos de menor a mayor. 2º Se determina la posición que ocupa cada cuartil mediante la fórmula: Qk = k (n/4)

NOTA
Los cuartiles son valores calculados, no observaciones en los datos. A menudo es necesario interpolar entre dos observaciones para calcular un cuartil con exactitud.
Debido a que no son afectados por observaciones extremas, la mediana y el rango intercuartil constituyen una mejor medida de la tendencia central y la dispersión de conjuntos de datos altamente asimétricos, en comparación con la media y la desviación estándar.
Ejemplos:
a) Dado el siguiente conjunto de datos: 2 ; 5 ; 9 ; 3 ; 13 ; 10 ; 11 ; 6 ; 7. ¿Cuál es el valor del tercer cuartil? 1° ordenamos los datos de menor a mayor: 2; 3; 5; 6; 7; 9; 10; 11; 13 n= 9 2º Se determina la posición que ocupa cada cuartil mediante la fórmula: Qk = k (n/4) Q3 = 3 (9 /4) Q3 = 6,75; En caso de ser un número decimal se aproxima al entero más cercano superior , que sería 7. Este valor indica la posición del cuartil 3. En nuestro caso el 7° valor sería : 2; 3; 5; 6; 7; 9; 10; 11; 13 Respuesta: el valor del tercer cuartil sería 10
b) Sea un conjunto de la edad de los veinte integrantes (N=20) de un club. Supongamos que el conjunto está ordenado:

-- El primer cuartil será el sujeto (N+1)/4=21/4=5,25.
Como es decimal, el cuartil será un número entre el X5=28 y X6=29.

El número decimal es el 5,25, por lo que i=5 y d=0,25. El cuartil 1 es:

-- El segundo cuartil es la mediana. Al ser un conjunto con un número par de elementos, el cuartil es la media de los sujetos N/2=20/2=10 y N/2+1=20/2+1=11.

Es decir, será la media de X10=34 y X6=37.

-- El tercer cuartil es el sujeto 3(N+1)/4=63/4=15,75. Como el número es decimal, el cuartil estará entre X15=52 y X16=53.

El número decimal es el 15,75, por lo que i=15 y d=0,75. El cuartil 3 es:

c) Calcular los cuartiles de la distribución de la tabla:

--Cálculo del primer cuartil


---Cálculo del segundo cuartil


--Cálculo del tercer cuartil


Deciles
Los deciles son los nueve valores que dividen la serie de datos en diez partes iguales.
Los deciles dan los valores correspondientes al 10%, al 20%... y al 90% de los datos.
D5 coincide con la mediana.
Cálculo de los deciles
En primer lugar buscamos la clase donde se encuentra

en la tabla de las frecuencias acumuladas.

Li es el límite inferior de la clase donde se encuentra el decil
N es la suma de las frecuencias absolutas
Fi-1 es la frecuencia acumulada anterior a la clase el decil
ai es la amplitud de la clase
ejemplo:




Percentiles
Finalmente los percentiles, también conocidos como centiles son otras de las Medidas de Posición más comunes y empleadas, utilizadas sobre todo para clasificación de datos correspondientes a las medidas de las personas, como la estatura, el peso, el diámetro craneal, etc. Igualmente, técnicamente, son definidos como ciertos valores que dividen en cien partes idénticas porcentualmente hablando los datos que han sido ordenados de forma sucesiva de menor a mayor. En cuanto a su denotación, ésta corresponde a la forma P1, P2…. Pn, no obstante son leídas como Percentil 10, Percentil 90, etc.
--Percentiles de Datos no agrupados Si se trata del cálculo de percentiles de datos no ordenados, se deberá tomar calcular en base a la siguiente fórmula:

k= 1,2,3,... 99
-- Percentiles de Datos Agrupados Por otro lado, si se desea calcular el percentil en base a datos que se encuentran agrupados, se deberá entonces emplear la siguiente fórmula:

Donde:
Lk = Límite real inferior de la clase del decil k
n = Número de datos
Fk = Frecuencia acumulada de la clase que antecede a la clase del decil k.
fk = Frecuencia de la clase del decil k
c = Longitud del intervalo de la clase del decil k
ejemplo:
Determinación del primer cuartil, el séptimo decil y el 30 percentil, de la siguiente tabla:

Estos resultados nos indican que el 25% de los empleados ganan salarios por debajo de $ 334; que bajo 541.57 gana el 57%de los empleados y sobre $359.88, gana el 70% de los empleados.
LA DESVIACIÓN
--LA DESVIACIÓN MEDIA
La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
La desviación media se representa por Dx
Ejemplo:
Calcular la desviación media de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Calculamos la media aritmética para poder hallar las desviaciones respecto a la media

Aplicamos la fórmula de la desviación media

Desviación media para datos agrupados
Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la desviación media es:
Ejemplo:
Calcular la desviación media de la distribución:

En primer lugar calculamos la media aritmética:
Incorporamos otra columna con los productos de las marcas de clase por sus frecuencias absolutas correspondientes y hacemos la sumatoria (457.5).
Por otro lado realizamos la sumatoria de las frecuencias absolutas (21)

Añadimos otra columna a la tabla con las desviaciones respecto a la media (|x - x|)

Agregamos otra columna con los productos de desviaciones respecto a la media por sus frecuencias absolutas correspondientes (|x - x| · fi) y calculamos su sumatoria (98.75)

Calculamos la desviación media

--LA DESVIACIÓN ESTÁNDAR
La fórmula de la desviación Típica o estándar (DE) es:

donde ∑ significa "suma de", x es un valor de un conjunto de datos, \muμmu es la media del conjunto de datos y N es el número de datos.
Puede parecer que la fórmula de la desviación estándar es confusa, pero tendrá sentido después de que la desglosemos. En las secciones subsecuentes explicaremos un ejemplo interactivo, paso a paso. Aquí hay una rápida vista previa de los pasos que estamos a punto de seguir:
Paso 1: calcular la media.
Paso 2: calcular el cuadrado de la distancia a la media para cada dato.
Paso 3: sumar los valores que resultaron del paso 2.
Paso 4: dividir entre el número de datos.
Paso 5: sacar la raíz cuadrada.
----La desviación típica se representa por σ.
ejemplo:
Calcular la desviación típica de la distribución:
9, 3, 8, 8, 9, 8, 9, 18
Calculamos la media aritmética
----- Desviación típica para datos agrupados
Para simplificar el cálculo vamos o utilizar las siguientes expresiones que son equivalentes a las anteriores.




Ejemplo:
Calcular la desviación típica de la distribución de la tabla:

Hemos añadido la columna xi · fi porque queremos hallar su sumatoria (1820), que después dividiremos por N (42) para obtener la media

Hemos añadido la columna x²i · fi porque queremos hallar su sumatoria (88050), que después dividiremos por N (42) y al resultado le restaremos la media aritmética al cuadrado (43.33²), y por último haremos la raíz cuadrada del resultado obtenido






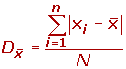
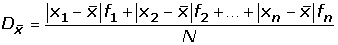
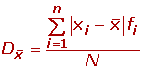
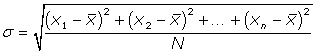
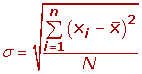
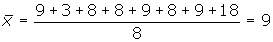

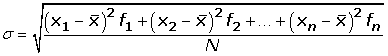




Comentarios